Gauss’s Law

The SI unit of electrical flux is:

Which law is used to derive the expression for the electric field between two uniformly charged large parallel sheets with surface charge densities $\sigma$ and $-\sigma$ respectively:

Applying Gauss theorem, the expression for the electric field intensity at a point due to an infinitely long, thin, uniformly charged straight wire is

A hollow charged metal sphere has radius $r$. If the potential difference between its surface and a point at a distance $3r$ from the centre is$V$, then electric field intensity at a distance $3r$ is:

An electric field $\mathrm{E}$ is present ${\perp }^{\mathrm{r}}$ to a square plate of side length $\mathrm{L}$. What is the flux passing through the plate?

A charge $\mathrm{Q}$ is distributed uniformly in a sphere (solid). Then the electric field at any point $\mathrm{r}$, where $\mathrm{r}<\mathrm{R}$ ( $\mathrm{r}$ is radius of sphere) varies as_____.

Two infinitely long parallel conducting plates having surface charge densities $+\mathrm{\sigma }$ and $-\mathrm{\sigma }$ respectively are separated by a small distance. The medium between the plates is vacuum, if ${\mathrm{\epsilon }}_{\mathrm{o}}$ is dielectric permittivity of vacuum, then the electric field in the region between the plates is-

A cylinder of radius $R$ and length $L$ is placed in a uniform electric field $E$ parallel to the cylinder axis. The total flux for the surface of the cylinder is given by

$\oint \overrightarrow{E.}\overrightarrow{ds}=\frac{Q_{net}}{{\epsilon }_o}$

E signifies the _____ passing through a certain area dS. $Q_{net}$ is the total amount of charge and ${\epsilon }_o$signifies the permittivity of the vacuum.

Derive Gauss's law from Coulomb's law.

Assertion: Gauss's law can't be used to calculate electric field near an electric dipole.
Reason: Electric dipole don't have symmetrical charge distribution.

Area vector is a vector quantity associated with each plane figure whose magnitude is

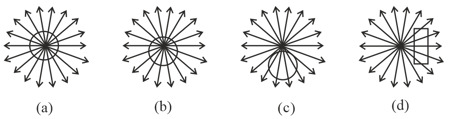
The black shapes in the figure below are closed surfaces. The electric field lines are in red. For which case, the net flux through the surfaces is non-zero?

Let the electrostatic field, $E$ at distance, $r$ from a point charge, $q$ not be an inverse square but instead an inverse cubic, e.g. $E=k\frac{q}{r^3}\hat{r}$, here $k$ is a constant. Consider the following two statements: (I) Flux through a spherical surface enclosing the charge is, $\varphi =\frac{q_{\mathrm{enclosed}}}{{\epsilon }_0}$. (II) A charge placed inside a uniformly charged shell will experience a force. Which of the above statements are valid?

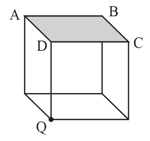
A point electric charge $Q$ is placed at a corner of a cube as shown in the figure. What is the electric flux passing through $ABCD$ of the cube? (${\in }_0$ is permittivity of free space)

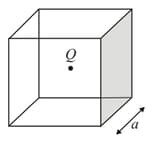
A point charge $Q,$ is placed at the center of a cube of side $a,$ in vacuum (permitivity $\left.{ϵ}_0\right).$ The flux of the electric field through the shaded face is given by

A sphere of radius $R$ carries a positive charge density $\left(\rho \right)$ that increases linearly with radial distance $r$ from the centre $(\rho \propto r).$ The radial dependence of the magnitude of electric field inside the sphere is given by

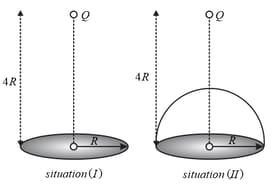
A positive point charge $Q$is placed (on the axis of the disc) at a distance of $4R$above the center of a disc of radius $R$as shown in situation $I.$The magnitude of electric flux through the disc is $\varphi .$Now, a hemispherical shell of a radius $R$is placed over the disc such that it forms a closed surface as shown in situation $\mathrm{II}.$The flux through the curved surface in the situation $\mathrm{II}$ taking direction of area vector along outward normal as positive is

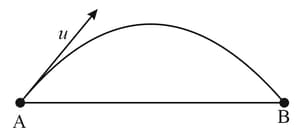
In the figure shown, there is a large sheet of charge of uniform surface charge density $\sigma$. A charge particle of charge $-q$ and mass $m$ is projected from a point $A$ on the sheet with a speed $u$ with angle of projection such that it lands at maximum distance from $A$ on the sheet. Neglecting gravity, find the time of flight.

The total flux through the faces of the cube with side of length $\mathrm{\alpha }$ if a charge $\mathrm{q}$ is placed at corner $\mathrm{A}$ of the cube is